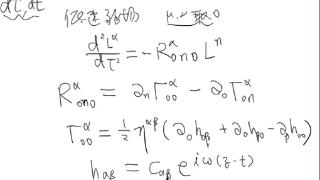测地偏离方程中为什么需要协变导数？《张朝阳的物理课》再访形变矢量

此前课程中，学习了如何在弱场低速近似下推出测地偏离方程，以及如何选取TT规范来推导引力波的两种模式。本节课将复习测地偏离方程，通过回顾协变导数和普通导数之间的区别与练习，重申在推导形变矢量的微分方程的过程中，可能发生混淆的一些谬误。

2月16日12时，《张朝阳的物理课》第二百三十七期开播，搜狐创始人、董事局主席兼CEO、物理学博士张朝阳坐镇搜狐视频直播间，首先回顾了微分几何中协变导数与普通导数的区别，然后通过对两条近邻的测地线作差，得到关于形变矢量的微分方程，再将普通微分算子换成协变微分算子，从而得到了完整的描述形变矢量的微分方程，它和测地偏离方程给出的结论是一致的。

（张朝阳讲解测地偏离方程）

协变导数和普通导数的联系

在微分几何中，各点处的基矢并不一定是相等的，尤其是在时空本身就是弯曲的情况下。基矢的变化也会引起时空中矢量的变化，为了描述矢量随着时空坐标发生微小变动后的变化量，需要引入协变微分的概念，它等于对矢量分量的普通微分加上由基矢变化所导致的修正项

最后一步中，交换了第二项的哑指标α和β，并用基矢的变化定义了克氏符

同理，可以定义矢量的协变导数为

这样定义之后，就能把矢量的协变微分所描述的微小变化量，写成它的协变导数与坐标微元的缩并，用逆变分量写成公式就是

两条相邻测地线的偏离速度的量级

假设有一粒子A沿着测地线运动，它的坐标x满足

它的四速度V在低速近似下可以近似取为(1,0,0,0)。在该粒子的临近处，有另一个粒子B沿着另一条测地线运动，它的坐标x'可以用

来描述，为了让符号更加简洁，将这两个坐标在同一仿射参数τ下的偏离用字母L记为

需要强调的是，由于选取的是相邻的测地线，偏离量L是一个小量，所以尽管它是两处时空坐标的差，仍然可以认为它是一个一阶张量，能同时满足x处和x'处的坐标变换规律，就好像坐标微元dx一样。因此，可以称这个偏离量L为形变矢量。

此前课程中，采用TT坐标规范后，得到了弱场近似下度规微扰在平面引力波中的形式

再加上低速近似，就能得到L所满足的方程

其近似解为

考虑低速近似下坐标时t接近于原时τ，所以偏离量的四速度具有量级

一般而言，引力波导致的度规微扰h可以取10^(-21)量级，即使频率能达到1000Hz，偏离量的四速度相比于偏离量本身也不过是10^(-18)量级，因此对于粒子B而言，它的四速度也依然近似为(1,0,0,0)。

在低速近似下推导测地偏离方程

前文论证了低速近似的合理性，现在再回过头来仔细研究一下偏离量所满足的方程（2）是如何导出的。对于两条测地线

在考虑了低速近似之后，上式变成

由弱场近似和TT规范给出的度规微扰式（1）可以直接算出克氏符在下标取为00时的分量恒为0：

这样就会得到一个看似平庸的结果

这样看起来形变矢量似乎是一个常矢量。但这里有一个概念性的问题：形变矢量的加速度在弯曲时空中应该用协变导数来描述，即

所以接下来需要把普通导数换成协变导数，为此，先来考察一阶协变导数和普通导数的关系

考虑到低速近似，对于四速度可以只取γ=0的一项

接下来计算二阶协变导数

已经知道，第一项中对L的二阶普通导数等于0，第三项和第四项中

所以第三项和第四项都是关于h的二阶小量，相比于第二项是可以忽略的。这样就得到了

再将克氏符具体地计算出来

代入上式后得到

到这里，用协变导数较为全面地描述了形变矢量的加速度。这时候再引入弱场近似，把协变导数近似为普通导数，才能得到非平庸的结果

进一步地，利用低速近似，可以把原时换成坐标时

这样就得到了上一节中（2）式的结果。它与之前的课上用测地偏离方程

给出的结论是一致的。测地偏离方程的意义十分重大，因为这里的形变矢量L是可以实际测量到的。引力波也可以用度规微扰h来描述，但度规并不是直接的可观测量，只有将微扰代入到黎曼曲率张量并解出测地偏离方程，才得到引力波所引起的偏离量，进而与实验数据进行对比。

据了解，《张朝阳的物理课》于每周周日中午12时在搜狐视频直播，网友可以在搜狐视频APP“关注流”中搜索“张朝阳”，观看直播及往期完整视频回放；关注“张朝阳的物理课”账号，查看课程中的“知识点”短视频；此外，还可以在搜狐新闻APP的“搜狐科技”账号上，阅览每期物理课程的详细文章。返回搜狐，查看更多