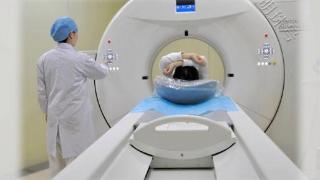
一文读懂安检机器的工作原理

过年的鞭炮声已经稀疏

浓浓的家乡情丝毫不减

春节小长假已接近尾声

人们开始踏上离乡的路

当你登上火车或者飞机之前

安检是一个必不可少的环节

不管你的行李箱中装的是家乡的特产

还是沉甸甸的知识

它们在通过安检机时

都将被工作人员看到

图源|pixabay

安检机究竟是怎样工作的？本文试图介绍现有的X射线安检设备的工作原理，为旅途中的读者提供一个一边消磨时光，一边增长知识的机会。01.单能X射线成像

首先，什么是X射线呢？

X射线是一种高能电磁波，通常人们把频率位于3×10¹⁶Hz~3×10¹⁹Hz(单光子能量约100eV~100keV，频率越高单光子能量越高)范围内的电磁波称为X射线。

X射线由德国物理学家伦琴(WilhelmConradRöntgen)于1895年发现，因此又被称为伦琴射线。

伦琴|图源Wikipedia

X射线照射到物体上会发生什么呢？

X射线具有很强的穿透能力，当它穿透物质时，与物质中的原子尤其是电子发生相互作用并损失能量，强度随透射深度呈现指数衰减。

我们暂时不考虑X射线如何与物质中的原子发生相互作用，而是重点关注射线强度的指数衰减，这里射线的强度指的是单位时间穿过单位横截面积的射线的能量(通俗地讲就是射线所含有的光子的密度)。

式中，I₀表示入射X射线强度，I表示穿透物质后X射线的出射强度，x为X射线在物体中行进的距离，μ为线性衰减系数，上式表明X射线穿透物质时呈现指数衰减。

如何通过这个原理窥探我们的行李箱呢？

X射线强度衰减可以用来成像。X射线穿过被检测的行李箱时强度发生衰减，考虑到行李箱里的东西不是均匀分布的，因此从不同位置穿过行李箱的X射线的强度就会有所差异，探测透射X射线的强度分布并将其转化为灰度图像，就可以得到能够反映被检测物体内部结构的图像了。

X射线穿过物质时强度呈现指数衰减，可以利用透射强度进行成像，展示物质的内部结构|图源[2]

考虑到被检测物体并不是均匀的，所以线性衰减系数μ也是空间位置的函数，我们可以用μ=μ(s)来表示，那么

对上式取对数，并且定义对数透射信号 t(d)为

透射X射线的强度图像其实就反映了不同位置t(d)的相对大小。02.双能X射线成像

事情到了这里似乎很完美了，我们可以根据射线强度的衰减成像，这样我们就得到了行李内部结构的一个轮廓。

可问题是，我们没有办法知道被检测物体的元素组成。

为什么要知道元素组成？为什么只看到物体的形状不够？

我们知道安检的目的是保护列车或飞机及其乘客的安全，因此安检希望着重关注一些危险品，比如爆炸物等，获得被检测物体的元素组成可以很好地帮助爆炸物的检测。

那么什么技术可以帮助我们获得物质的元素组成的信息？

双能X射线成像同时探测一高一低两种能量的X射线穿过物体后的强度，进一步获得物体的元素组成的信息。

那么它的工作原理是什么？

单能量X射线成像决定于线性衰减系数μ和厚度x的乘积，通常原子序数大的物质μ大，具有大的原子序数的薄片可能和具有较小原子序数的厚的材料产生相同的效果，因此单能成像很难分辨物质的元素组成，如图所示

物质的线性衰减系数μ 与材料的原子序数和 X射线的光子能量有关，为了让分析更简单，我们暂时先考虑一个均匀的物质A，A的线性衰减系数可以表示成 α,β两种参考物质线性组合

对于选定的参考物质，μα(E)和μβ(E)是已知的，上式两边同时乘Lᴀ就得到了对数透射信号 tᴀ(E)，它也是能量的函数

式中Lα和Lβ是线性组合系数和Lᴀ的乘积，对于高能和低能射线分别测量 tᴀ(E)，并且解出Lα和Lβ，可以根据比值 Lβ/Lα确定图像上某一点的有效原子序数。

有效原子序数可以在一定程度上反映物质真实的原子序数，而我们知道，每种元素和该元素原子的原子序数是一一对应的，这样我们就确定了物质元素组成的信息。根据有效原子序数的数值给图像上色，就得到了假彩色的安检图像，如下图。

双能X射线成像给出的假彩色图像，图中金属、合金和硬塑料为蓝色，密度较低的物质展示为绿色或橙色|图源[4]

下图展示了一种双能X射线安检设备的布局。X射线管发射出连续谱X射线(包含多种频率，即包含多个能量)。穿过物体后的射线首先被低能探测器接收，接着穿过一块薄的铜片，铜片可以吸收较低能的射线，于是只有能量较高的部分穿过铜片到达高能探测器。这样人们就分别获得了高能和低能射线的信号。

一种双能X射线安检设备的布局|图源[3]03.多视角X射线安检技术

通常我们的行李箱被塞得很满，在射线通过的路径上有不止一个物体，上面的方法对物体仅沿一个方向投影，很难分辨重叠的物体。

那么如何解决物体的重叠问题呢？

就像人的双眼可以从不同的视角观察一个物体一样，人们发展了多视角成像技术。人们可以根据被检测物体的不同视角的二维图像，部分地获得物体的三维信息，可以有效解决重叠问题。此外，多视角成像技术还可以提高双能安检设备对原子序数判别的准确性。

现有的多视角X射线安检设备包括单射线源多视角模型和垂直式多视角模型等。下图展示了这两种模型的结构。

单射线源多视角模型 |图源[5]

上图布局将同一射线源发出的射线分成平行的两束，分别照射在传送带的不同位置上，当被检测物体在传送带上依次通过两束射线照射的区域时，人们就得到了从两个方向观察的X射线透射图像。

垂直式多视角模型 |图源[6]

上图布局在两个互相垂直的方向上放置射线源，从垂直的两个方向上获得被检测物体的透射图像，根据两个垂直视角的图像可以较为准确地重建出被检测物体的三维信息。04.CT安检技术

多视角X射线成像技术只能获得若干个视角的图像，重建物体三维信息的能力仍然有限，有没有更好的办法呢？

计算机断层扫描，也就是CT安检技术，从多个视角获得物体的二维图像，能重建物体的三维信息，可以解决物体重叠和遮挡的问题，提高物质判别的准确性，下面我们来看它的原理。

CT技术从多个视角照射X射线，获得被检测物体沿各个方向的投影

为了简化问题，我们只考虑被检测物体是二维物体的情形，它的线性衰减系数是μ(x,y)。如果我们只沿一个方向照射X射线，不妨将这个方向记为θ，那么我们可以得到沿这个方向的投影，如下图所示

图源[7]

沿θ方向的对数透射信号用公式表达，就是下面这样

如果我们旋转X射线，正如上面的动图那样，就得到了被检测物体沿各个方向的投影，也就是说t(θ,r)是射线的投影方向θ 和射线穿过物体位置r的函数。

经过一定的推导可以得到，t(θ,r)对r作一维傅里叶变换，其实就和 μ(x,y)对x,y作二维傅里叶变换后再沿着θ方向“切片”的结果一致

下图对上面的公式进行了形象地说明，从左至右分别是沿着θ方向进行X射线成像得到t(θ,r)、将t(θ,r) 沿θ方向放置得到二维图像、此二维图像就是μ(x,y)对x,y的二维傅里叶变换。

图源[7]

傅里叶变换简介

傅里叶变换是一种数学变换，它将一个函数分解成它的频率分量 (也可以理解为将一个函数用平面波作为基函数展开)，每一个频率分量表示函数的一种整体结构特性。一个函数f(x)的傅里叶变换F(k)以频率k为自变量，表示该频率分量在f(x)中的权重。一个函数和它的傅里叶变换包含相同的信息。

上面的公式上下两行分别是傅里叶正变换和逆变换

平面波概念图|图源pixabay

到了这里，我们就得到了重建被检测物体三维信息的方法，但为了简单起见，我们依然只讨论二维物体。重建物体信息可以尽量将二维傅里叶逆变换用t(θ,r)来表示

如果用公式表达，则根据各方向投影重建物体信息的过程是

上面的公式中，最下面一行表示对T(θ,ω) 在极坐标系做二维傅里叶逆变换 (这里的极坐标v=-ωsinθ，和惯例不同)，上面两行则表示对F(u,v) 的二维傅里叶逆变换。

利用极坐标系下傅里叶变换函数的对称性，T(θ,ω)=T(θ+π,-ω)，上面的公式可以变成

这个方法我们可以用下面的流程图展示出来。

我们已经获得了沿着各个方向的投影t(θ,r)，注意到对于二维物体每一个固定θ的投影都是r的一维函数。

我们将这些函数对r做傅里叶变换，再按照圆周的方式排列起来，就得到了物体的二维傅里叶变换。我们再进行傅里叶逆变换，就获得了物体原本的信息。

利用傅里叶变换重建CT图像|图源Wikipedia

当然，这是十分理想的情况，在实际应用中，安检机的设计者们还需要考虑很多工程上的问题，比如信号降噪、模糊修正等等。

本文介绍了单能X射线成像技术，利用X射线穿过物质时的指数衰减特性成像，得到的图像反映了被检测物体的内部结构。

为了便于判别物质的元素组成，人们研发了双能X射线成像技术；为了解决重叠问题，人们研发了多视角X射线安检技术；而CT技术被应用于安检，帮助人们准确地重建物体的三维信息。

技术的进步是为了保障旅途的安全，祝愿大家旅途愉快，在新的一年心想事成！